什么是實時頻譜儀（RTSA）？

頻譜分析儀是射頻微波設計和測試工作中的常用儀器，它能夠幫助電子工程師完成頻譜觀測、功率測試以及復雜信號解調分析等工作。所謂實時頻譜儀（Real-Time Spectrum Analyzer - RTSA）就是指能實時顯示信號在某一時刻的頻率成分及相應幅度的分析儀，它能夠幫助電子工程師完成頻譜觀測、功率測試以及復雜信號解調分析等工作。

實時頻譜儀采用快速傅里葉變換(FFT)來實現頻譜測試。在信號處理過程中能夠完全利用所采集的時域采樣點，從而實現無縫的頻譜測試及觸發。由于實時頻譜儀具備無縫處理能力，使得它在頻譜監測，研發診斷以及雷達系統設計中有著廣泛的實時頻譜儀提供豐富的顯示功能，包括光譜圖、概率密度譜和時間功率等多種顯示方式。

長久以來，因為實時頻譜解決了傳統頻譜儀不具備的瞬態信號分析功能，從而被很多人推崇，甚至帶上了無所不能的光環。認為實時頻譜能夠看到一切瞬態信號，并且精確無比。

為了更好地理解實時頻譜儀 RTSA 的功能，我們務必看一看傳統的頻譜分析儀接收機的體系結構及其優缺點。

實時頻譜儀的特性

實時頻譜儀普遍采用快速傅里葉變換FFT來實現頻譜測量。快速傅里葉變換FFT技術并不是實時頻譜儀的專利，其在傳統的掃頻式頻譜儀上亦有所應用。但是實時頻譜儀所采用的快速傅里葉變換FFT技術與之相比有著許多不同之處，同時其測量方式和顯示結果也有所不同：

高速測量：頻譜儀的信號處理過程主要包括兩步，即數據采樣和信號處理。實時頻譜儀為了保證信號不丟失，其信號處理速度需要高于采樣速度。

恒定的處理速度：為了保證信號處理的連續性和實時性，實時頻譜儀的處理速度必須保持恒定。傳統頻譜儀的FFT計算在CPU中進行，容易受到計算機中其它程序和任務的干擾。實時頻譜儀普遍采用專用FPGA進行FFT計算，這樣的硬件實現既可以保證高速性，又可以保證速度穩定性。

頻率模板觸發（Frequency Mask Trigger）：FMT是實時頻譜儀的主要特性之一，它能夠根據特定頻譜分量大小作為觸發條件，從而幫助工程師觀察特定時刻的信號形態。傳統的掃頻式頻譜儀和矢量信號分析儀一般只具備功率或者電平觸發，不能根據特定頻譜的出現情況觸發測量，因此對轉瞬即逝的偶發信號無能為力。因此傳統掃頻頻譜儀和實時頻譜分析儀各自有著自己的應用場景。

豐富的顯示功能：傳統頻譜儀的顯示專注在頻率和幅度的二維顯示，只能觀察到測量時刻的頻譜曲線。而實時頻譜儀普遍具備時間，頻率，幅度的三維顯示，甚至支持數字余輝和頻譜密度顯示，從而幫助測試者觀察到信號的前后變化及長時間統計結果。

實時頻譜儀主要應用

實時頻譜儀能夠在實時分析帶寬之內無縫地進行快速傅里葉變換FFT計算和頻譜觸發，因此十分有利于瞬態信號的捕獲和分析，在頻譜監測，雷達系統設計，跳頻電臺測試，振蕩器研發等領域有著廣泛的應用。

以下是幾種典型應用場景下的測試效果：

實時頻譜儀跳頻雷達信號檢測

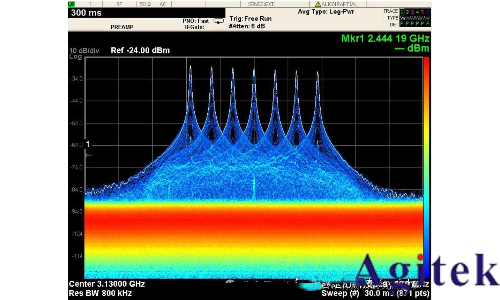
實時頻譜儀脈沖信號時域頻域分析

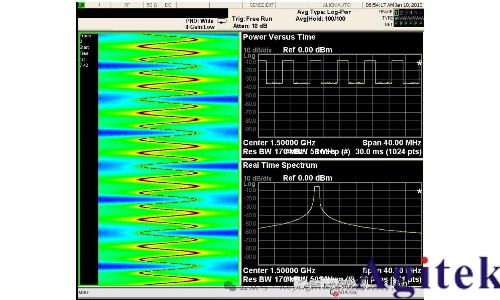
實時頻譜儀振蕩器鎖定過程分析

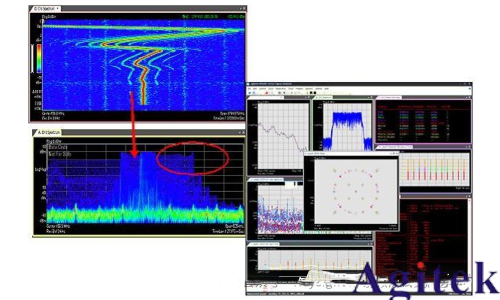
掃描調諧接收機-傳統的頻譜分析儀接收機的體系結構

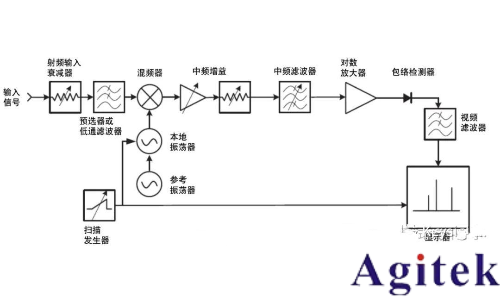
圖 4. 超外差頻譜分析儀/掃描調諧頻譜接收機

超外差頻譜分析儀也稱為掃描調諧頻譜分析儀。外差意味著混頻，在這個系統中，射頻輸入信號與本振信號混頻，將輸入信號從較高頻率轉換為較低頻率，即中頻（IF）。信號幅度通過包絡檢測器檢測并顯示為垂直點。

為了控制水平/頻率軸的顯示，我們使用斜坡/掃描發生器來控制運動，它還可以將本振調諧到預期頻率。通過設置掃描時間和頻率掃寬，可以控制本振調諧速率。頻譜分析儀的前端配有信號調理電路，包括衰減器和預選器（低通濾波器）。這些電路的作用是確保輸入信號在到達混頻器之前處于最佳電平。前端預選器有助于阻止帶外噪聲，從而改善接收機的動態范圍和靈敏度。調諧本振為接收機提供更好的選擇性。它可以很容易地阻止不需要的帶外信號，這就是超外差接收機具有出色動態范圍的原因。

由于斜坡發生器以固定速率進行掃描，因此可以在頻率掃寬上精確控制掃描時間。通過控制掃描速率，接收機能夠以超過快速傅里葉變換（FFT）分析儀的掃描速度掃描超大掃寬。

超外差接收機的最大缺點是它可能錯過間歇信號內容，尤其是寬帶數字調制信號。
另一個問題是，在窄分辨率帶寬（RBW）下掃描時間會明顯變長。

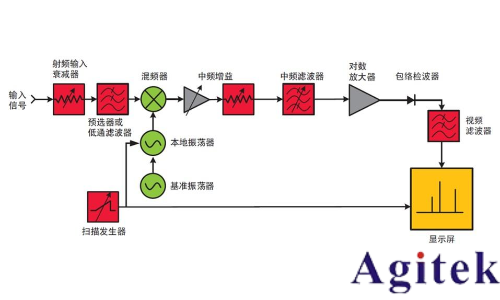
FFT分析儀/接收機

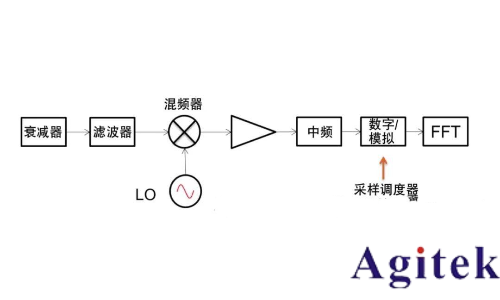
圖 5. FFT頻譜分析儀速覽

FFT分析儀/接收機專門用于處理寬帶信號。它的前端有一個數據塊轉換，數據塊轉換的大小由中頻帶寬和 ADC采樣率決定。本地振蕩器（LO）不是連續進行調諧，而是在頻率掃寬內步進調諧。在本振調諧到正確的頻率后，接收機通過模數轉換器（ADC）對數據進行采樣，再將采樣結果轉換為 I/Q 對（同相正交），并放入適當的 FFT時間幀內，然后將時域幀轉換為 FFT頻譜數據，最后將頻譜結果發送給顯示器，如此周而復始地執行這一過程。這是一個串行操作，因此在兩次屏幕更新之間會間隔一段時間，輸入端在此期間內不會捕獲信號。這段時間稱為靜寂時間，持續時間的長度不可預計。

由于它是數據塊轉換，因此數據塊或信息帶寬內的信號（例如數字解調信號）將被完整捕獲以供進一步分析。FFT 是分析寬帶數字信號的理想選擇；它可以基于信號技術指標重現數字接收機特性，如 LTE信號測試。

由于 FFT引擎無法在特定時間幀內完成其操作，因此無法精確控制 FFT接收機的掃描時間。
如果信號帶寬大于接收機的信息帶寬，則需要對信號進行拼接，這樣可能導致丟失部分寬帶信號內容。

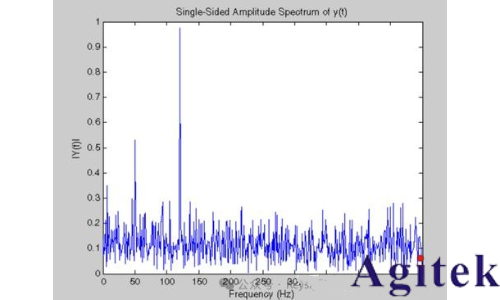
實時頻譜儀（RTSA）

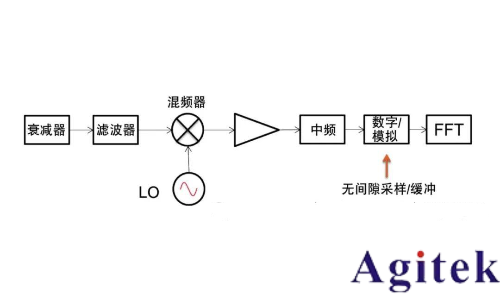
圖 6. 實時頻譜儀

實時頻譜儀是一種沒有靜寂時間的 FFT分析儀。接收機停留在感興趣的頻率掃寬內，該掃寬受到實時頻率帶寬的限制，沒有調諧或步進。它具有足夠大的信號緩沖區、FFT計算工具和顯示工具，可在后續數據幀進入之前處理完上一個數據幀并清空存儲器。

在其捕獲帶寬內，它可以檢測各種瞬態信號、動態信號和射頻脈沖。

但是，實時頻譜儀RTSA受到帶寬的限制。如果接收機試圖測量超出其實時帶寬的信號，則必須調諧本振，此時它不再是實時或無間隙的。

由于實時頻譜儀 RTSA 沒有調諧，要檢測的信號可能不會位于中心頻率，并且它檢測到的信號電平可能不像使用傳統頻譜分析儀時那么準確，因此我們不建議采用實時頻譜儀 RTSA 來進行準確的功率測試。

實時頻譜儀RTSA信號流和數據處理

實時頻譜儀RTSA 的基礎是 FFT處理，但它沒有 FFT分析儀的靜寂時間。它處理和顯示信號的速度快于 ADC 在給定信息帶寬下填滿循環緩沖區的速度。當然，實時頻譜分析儀RTSA 也有不足之處，它始終采用固定調諧并且帶寬有限。在給定帶寬下，它不會錯過任何信號。在檢測瞬態信號時，它是理想的選擇。

除了超快速的 FFT計算工具和足夠大的循環存儲緩沖區之外，實時頻譜儀RTSA 中最關鍵的技術稱為重疊 FFT。采用重疊 FFT，RTSA 能夠可靠地檢測具有隨機占空比的窄脈沖。

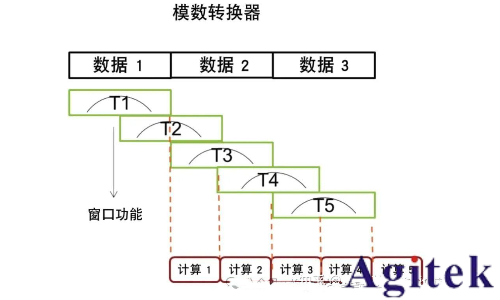
圖 7. 實時頻譜分析儀RTSA信號處理流程

以上是實時頻譜儀 RTSA信號流。首先，ADC 從中頻鏈路中采樣數據，并將它們打包到每個數據幀內。

實時頻譜RTSA 不是一次處理一幀的原始數據，而是將原始數據幀（數據 1、數據 2、數據 3 ……）重新排列成新的 FFT幀（T1、T2 ......）。從 T2 開始，RSTA 會從 T1 獲取一部分樣本并將其與新數據（數據 2 獲取的一部分）合并，構成 T2；同理，從前面的 T2 獲取一部分樣本，再從數據 2 獲取一部分新樣本，構成 T3。這種操作叫做重疊 FFT，它保證發生在數據 1 和數據 2 邊緣的信號會正確位于下一個 FFT 的中心，以確保正確檢測到信號。

將信號移動到幀中心是為了防止窗口功能濾除掉數據幀/時間記錄邊緣的有用信號。為了便于說明，我們進行 FFT 計算和顯示的速度是將數據保存到緩沖區速度的兩倍。

FFT重疊問題

為了理解何為重疊處理，首先可以看下圖。

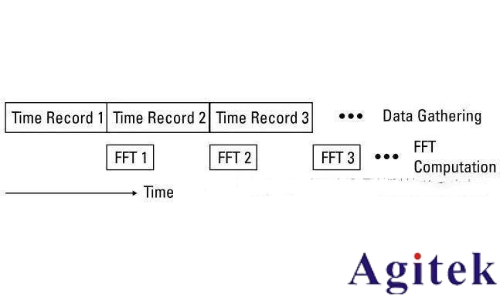
觀察到一段數據記錄完成后，立刻進行FFT處理，其中信號采集的時間比FFT計算時間長得多。仔細觀察便可發現，當一個FFT處理流程結束后，大部分時間都處于閑置狀態。如果此時不是等待一個全新采集信號，而是將目前最新的信號記錄與一些舊數據重疊，那么在計算FFT的同時將獲得一個新的頻譜，下圖中說明了這種重疊處理。

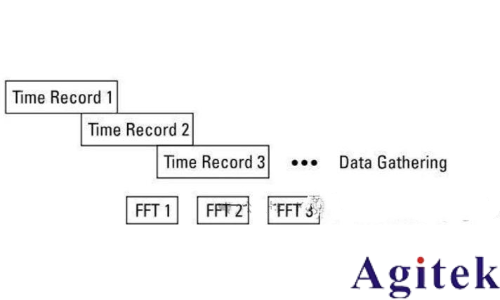
為了了解重疊處理的好處，我們可以看一個例子。

例如計算設備每隔十分之幾秒才能更新一個FFT計算得到的頻譜，因為其中沒有涉及重疊處理，分辨率被限制在10Hz左右。如果需要增大頻率分辨率，則需要增大采樣率，同時減小FFT的計算時間，而這樣會大大增加硬件的成本。如果是通過重疊處理，則可以把分辨率無限減小，這樣會產生一個問題：由于重疊的信號包含前段采集的舊數據，因此并不完全正確，不過其確實可以指示信號變化的方向和幅值，而且準確的頻譜也可以等后續非實時計算得到。總結來說，重疊處理能夠在當前硬件的條件下，對分辨等參數做一定程度的補充。

FTT重疊極大地提高了捕獲窄脈沖或瞬態信號的概率。在下面的屏幕顯示中，一個顯示接收機在兩次更新之間有靜寂時間而沒有 FFT重疊，另一個顯示的是有重疊 FFT 的RTSA。

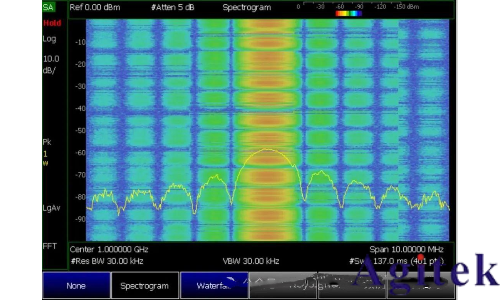
圖 8. 沒有 FFT重疊，屏幕更新之間存在靜寂時間

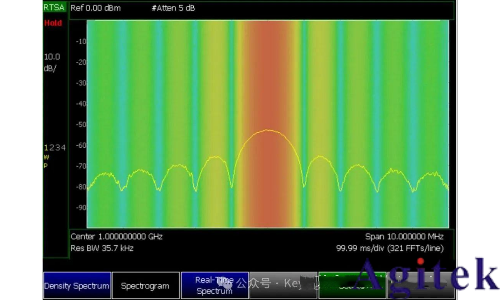
圖 9：無間隙進行捕獲的 FFT重疊

長久以來，因為實時頻譜解決了傳統頻譜儀不具備的瞬態信號分析功能，從而被很多人推崇，甚至帶上了無所不能的光環。認為實時頻譜能夠看到一切瞬態信號，并且精確無比。

然而從實時頻譜的具體實現技術出發，它并不是萬能的。準確地說，實時頻譜的準確測量對于信號的持續時間是有要求的，對于少數低于這個要求的信號，實時頻譜也無法完全準確地進行測量。

下面我們仔細描述一下這個問題。

什么是100%截獲概率（POI）？

在無線射頻信號分析中，截獲概率(POI)表示信號有可能被截取和充分捕獲、分析所需要的存在時間。

作為參考，加拿大出口管制指南2013年12月"提供了以下定義：“發現概率也稱為截獲概率或捕獲概率。100%發現概率的持續時間等于特定電平測量不確定度所需的最小信號持續時間。

Keysight應用說明“理解和應用實時頻譜分析中的截獲概率'在下面的摘錄中提供了進一步的說明：在信號分析儀的性能Q參數中，POI通常表示為一個信號的最小持續時間，要求該信號若高于儀器的噪聲系數，則該信號可以以100%的概率觀察到并進行準確地測量。

前提：設置FMT的觸發電平并使用FMT去觸發一個瞬態的信號

頻率模板觸發 Frequency Mask Trigger（FMT）觸發后頻譜儀測到的瞬態信號幅度與其穩態時相同

要滿足上述條件，信號必須持續一定時間，該時間稱為100%截獲概率下的最短持續時間。

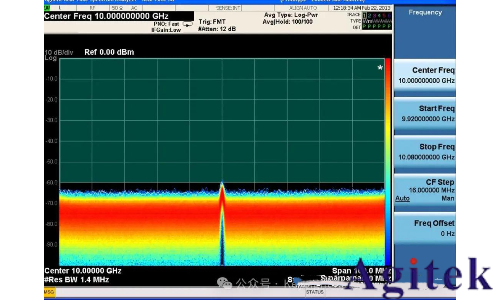
通常使用的窗函數以及不同的特性

五種主要的窗口函數

?也叫加權函數

?用于抑制時域旁瓣

?邊帶影響: 損傷信噪比

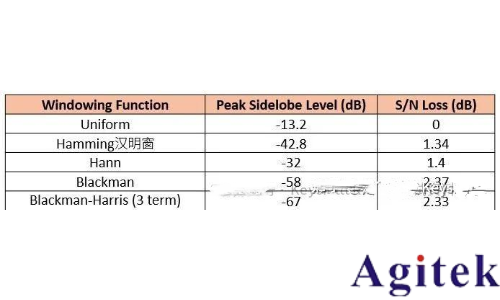
Hamming Window 漢明窗的原理

漢明窗口 （Hamming Window）是一種常用的數字信號處理技術，為了提高分辨率，需要對接收到的信號進行一定的處理。其中一個重要的步驟是快速傅里葉變換 (Fast Fourier Transfomm, FFT)，通過FFT可以將回波信號從時域轉換到頻域，以便更好地分析和處理。然而，在進行FFT時，由于信號長度有限，會導致頻譜上出現泄漏(spectral leakage）現象，即信號在頻域上呈現出明顯的畸變，初值和諧波等非理根特征。為了減少這種泄漏，可以采用漢明窗口來對原始信號進行加商處理，其主要作用是在時域上對信號進行平滑加權，抑制信號的端點泄漏，以減小FFT過程中信號的泄漏現象，從而得到更精確的頻域信息。

時域和頻域

時域和頻域是信號處理中兩個基本的概念：

時域(Time Domain)指的是信號隨著時間變化的情況，即信號在時間軸上的表現形式。例如音頻信號在時域下的圖形可以顯示聲音如何隨著時間變化，而圖像信號在時域下的圖形可以顯示圖像的像素值如何隨著時間變化。

頻域 (Frequency Domain）指的是信號在頻率空間中的表現形式，表示信號包含哪些頻率成分及其對應的強度。以音頻信號為例，在頻域下的圖形（一般稱為頻譜）可以顯示聲音分布在哪些頻率及其比例，即能夠反映出聲音中各個音調的高低與響度大小，將時間與頻率進行有效分離，方便對信號進行后續處理。

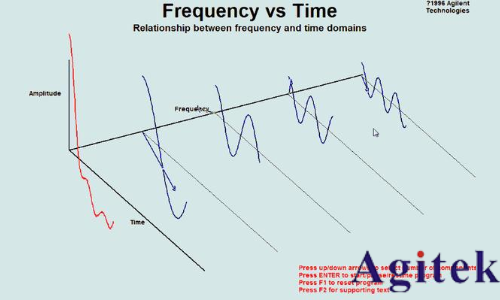
在數字信號處理中，信號通常會在時域和頻域之間進行轉換。例如，通過傅里葉變換（FFT）可以將時域的信號轉換到頻域中，從而更好地理解信號的特性。在頻域下，信號可以通過浪波等方法進行處理，然后再通過傅里葉逆變換(IFT) 口到時域中進行應用。

什么是多普勒效應 (Doppler effect)?

多普勒效應 (Doppler effect) 是指當波源與觀察者相對運動時，觀察者接收到的波的頻率與波源發出的頻率不同的現象。在多普勒效應中，當波源向觀案者移動時，觀案者會接收到比波源發出時重高的頻率，這被稱為藍移 (blue shift);反之，當波源遠離觀察者時，觀察者接收到比波源發出時更低的頻率，這被稱為紅移(red shirt)。藍移和紅移的現象可以在各種波動中觀察到，如聲波電磁波等。

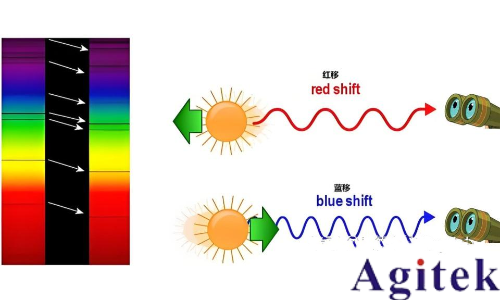
多普勒效應在現代科技中有看廣泛的應用，如測速雷達、醫學超聲診斷、天文學等。在衛星通信中，由于衛星和地面站之間的相對運動，多普勒效應會導致信號的頻率發生變化，因此必須對信號進行補償以確保正常通信。

Hamming Window 漢明窗函數和頻響

時域和頻域加窗的效果是相同的-減小頻率泄露

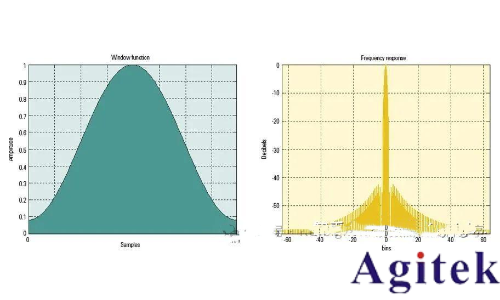
漢明窗函數的形狀（左）及其相關的頻率響應（右）

重疊的FFT處理

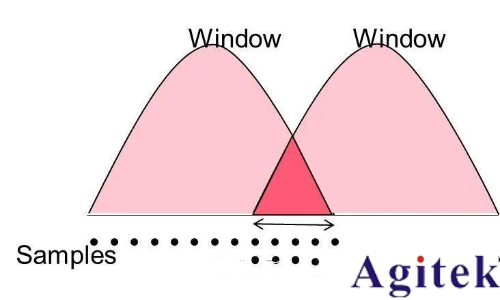
重疊的FFT

實時頻譜儀的基本原理是分段采集數據，然后進行高速FFT處理。

我們知道，每次FFT處理的時域樣點都是有限長度，而有限的時間長度在頻域上將產生周期延拓或者說頻譜泄露。因此FFT處理之前都需要對時域樣點就行加窗處理，加窗處理將導致窗兩邊的數據權重降低甚至歸零，導致部分信息丟失。

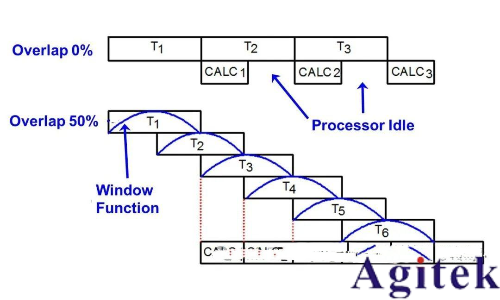
為了補償加窗造成的信號丟失，實時頻譜儀中普遍采用重疊幀的FFT處理。兩段相鄰的時域數據將部分重疊然后進行FFT計算，這樣兩段相鄰數據的窗函數可以相互補償，從而保證信號不丟失。

Keysight的實時頻譜儀中，將在FFT速度和采樣速率允許的情況下進行最大程度的重疊處理。

?FFT時域截短造成頻域擴展
?通過加窗抑制頻譜擴展
?加窗造成部分數據權重降低?通過overlap來補償加窗造成的分量權重降低

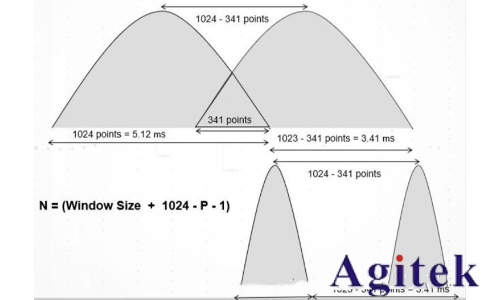
實時頻譜儀中FFT的長度一般是固定的1024點，而窗的寬度是可以調整的（32-1024）。信號如果需要保證幅度被準確測量，那么其持續時間最短需要從第一個窗的左邊緣一直到第二個窗的右邊緣。因此從圖上可以看粗，信號最短持續時間取決于FFT的長度，重疊的點數以及所選擇的窗的寬度。減小窗的長度，可以降低信號最短持續時間的要求。

下面用一個例子闡述合成窗是如何重建信號的。下圖是一個時域轉頻域加窗的過程。

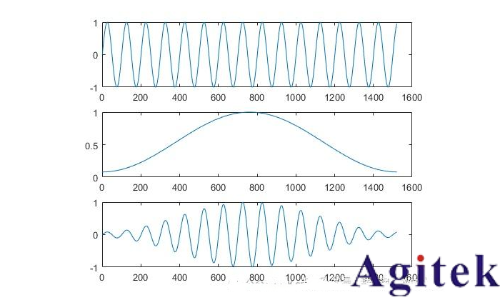
可以看到，經過加窗后，能量有所衰減。加一個合成窗，且overlap-add，便可以補回能量。如下圖所示:

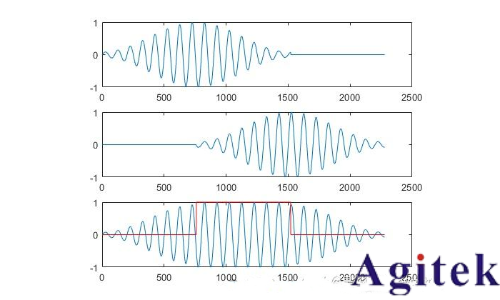
可以定性看到，在經過overlap，邊界處的信號補回原始幅度了。此處是比較巧妙，分析窗用hamming窗，overlap采用50%，則在合成的時候，就不需要額外加窗了，直接overlap-add就好。

根據完美重建公式，合成窗的選擇，不僅跟分析窗有關，還和overlap有關。不同的overlap要采用不同的合成窗。

若信號持續時間短于一個FFT的長度

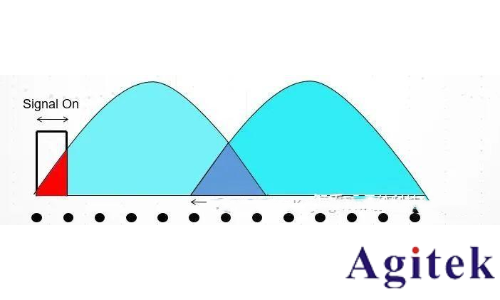
剛才我們講到為了保證幅度精度，信號有一個最短持續時間。那么當信號持續時間低于這個閾值時，會發生什么情況呢？

我們知道時域樣點的能量，在經過FFT變換之后將在頻域展開，其能量是守恒的。不管時域數據持續多長，FFT之后再頻域都是1024個點。因此，當信號持續時間短于一個FFT長度時，它在頻域的功率將降低。降低的程度取決于途中紅色區域的面積和淺藍色區域面積的比例。即2個條件：首先是信號持續時長，其次是信號在窗函數中的位置。同樣的信號時長，出現在窗邊緣和窗中心，其FFT后的功率將差異很大。

?FFT之后得到的功率將降低
?功率降低的程度取決于兩個因素：信號持續時長以及出現的位置
?綜合來看，就是下圖中深紅色面積與藍色面積之比

下面我們將看到仿真計算結果。

當四分之一格FFT長度的信號出現在窗中央時，其功率將下降4.125dB；但是當信號出現在窗邊緣時，其功率將下降29.129dB。

例如：

?信號時域采樣率為200 MHz, 1024 點FFT?完全保證幅度精度的信號持續時間為5.12 us?場景1 ?信號出現在窗的正中央，時長為 ? 窗長度（藍色）?場景2 ?信號出現在窗的左邊緣，時長為 ? 窗長度（紅色）

經過FFT之后的頻譜中功率下降：

場景1: -4.125 dB

場景2: -29.129 dB

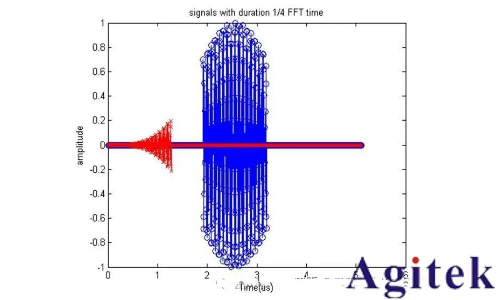
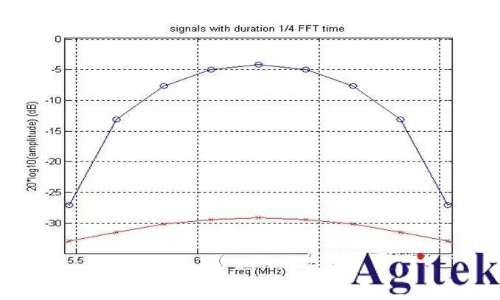
實際用信號源也很好驗證

利用信號源的脈沖功能輸出一個固定幅度的脈沖，通過調節脈寬，觀察不同脈寬下實時頻譜儀上測到的信號頻譜，可以發現當脈寬低于一定程度的時候，信號功率將不同程度地下降。

同一個信號源輸出等功率脈沖：

?脈寬大于特定時長時功率準確
?脈寬逐步減小時，頻譜上測到的功率逐步降低

頻譜分析儀和信號分析儀有什么區別？

頻譜分析儀和信號分析儀這兩個術語往往可以互換使用，不過兩者在功能和能力上還是有一定區別。頻譜分析儀主要用于測量輸入信號的幅度與頻率的關系。 信號分析儀則是同時測量輸入信號在單個頻率上的幅度和相位。 當今的分析儀可進行更全面的頻域、時域和調制域信號分析，用“信號分析儀”來描述更為準確。

頻譜分析儀

頻譜分析儀是什么？

頻譜分析儀測量在儀器的整個頻率范圍內輸入信號幅度隨頻率進行變化的情況。其最主要的用途是測量已知和未知信號的頻譜功率。

矢量信號分析儀測量在儀器的中頻帶寬內輸入信號在單一頻率上的幅度和相位。其最主要的用途是對已知信號進行通道內測量，例如誤差矢量幅度、碼域功率和頻譜平坦度。

信號分析儀同時執行頻譜分析儀和矢量信號分析儀的功能。
頻譜分析儀有什么用途？

頻譜分析儀可在整個頻率范圍內測量輸入信號的幅度與頻率的關系，從而確定信號的功率。 頻譜分析儀能夠進行噪聲系數和信噪比（SNR）等測試，表征器件的性能及其對整體系統性能的貢獻。

信號分析儀能夠做什么？

信號分析儀能夠測量輸入信號在單個頻率上的幅度和相位。 信號分析儀將掃頻調諧頻譜分析儀的超大動態范圍與矢量信號分析儀（VSA）的強大功能相結合，能夠執行信道內測量，例如需要幅度和相位信息的誤差矢量幅度（EVM）測量。